Psychology 105
Richard Lowry
©1999-2002
Some Basic Statistical Concepts and Methods
for the Introductory Psychology Course
Part 6

Concepts of Correlation

   Correlation refers to the relationship that exists between two variables, X and Y, in the case where each particular value of Xi is paired with one particular value of Yi. For example: the measures of height for individual human subjects, paired with their corresponding measures of weight; the number of hours that individual students in a course spend studying prior to an exam, paired with their corresponding measures of performance on the exam; the amount of class time that individual students in a course spend snoozing and daydreaming prior to an exam, paired with their corresponding measures of performance on the exam; and so on.

   Fundamentally, it is a variation on the theme of quantitative functional relationship.The more you have of this variable, the more you have of that one. Or conversely, the more you have of this variable, the less you have of that one. Thus: the more you have of height, the more you will tend to have of weight; the more that students study prior to a statistics exam, the more they will tend to do well on the exam. Or conversely, the greater the amount of class time prior to the exam that students spend snoozing and daydreaming, the less they will tend to do well on the exam. In the first kind of case (the more of this, the more of that), you are speaking of a positive correlation between the two variables; and in the second kind (the more of this, the less of that), you are speaking of a negative correlation between the two variables.

   Here is an introductory example of correlation, taken from the realm of education and public affairs. If you are a college student in the United States, the chances are that you have a recent and perhaps painful acquaintance with an instrument known as the Scholastic Achievement Test (SAT, formerly known as Scholastic Aptitude Test), annually administered by the College Entrance Examination Board, which purports to measure both academic achievement at the high school level and aptitude for pursuing further academic work at the college level. As those of you who have taken the SAT will remember very well, the letter informing you of the results of the test can occasion either great joy or great despair. What you probably did not realize at the time, however, is that the letter you received also contributed to the joy or despair of the commissioner of education of the state in which you happened that year to be residing.

   This is because every year the College Entrance Examination Board publicly announces the state-by-state average scores on the SAT, and every year state education officials rejoice or squirm over the details of this announcement, according to whether their own state averages appear near the top of the list or near the bottom. The presumption, of course, is that state-by-state differences in average SAT scores reflect underlying differences in the quality and effectiveness of state educational systems.

   And sure enough, there are substantial state-by-state differences in average SAT scores, year after year after year. The differences could be illustrated with the SAT results for any particular year over the last two or three decades, since the general pattern is much the same from one year to another. We will illustrate the point with the results from the year 1993, because that was the year's sample of SAT data examined in an important research article on the subject.
Powell, B., & Steelman, L. C. "Bewitched, bothered, and bewildering: The uses and abuses of SAT and ACT scores." Harvard Educational Review,66, 1, 27—54.
See also Powell, B., & Steelman, L. C. "Variations in state SAT performance: Meaningful or misleading?" Harvard Educational Review,54, 4, 389—412.
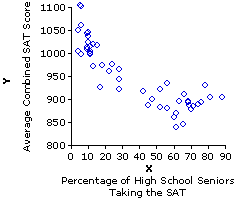
   Among the states near the top of the list in 1993 (verbal and math SAT averages combined) were Iowa, weighing in at 1103; North Dakota, at 1101; South Dakota, at 1060, and Kansas, at 1042. And down near the bottom were the oft-maligned "rust belt" states of the northeast: Connecticut, at 904; Massachusetts, at 903; New Jersey, at 892; and New York, more that 200 points below Iowa, at 887. You can easily imagine the joy in DesMoines and Topeka that day, and the despair in Trenton and Albany. For surely the implication is clear: The state educational systems in Iowa, North Dakota, South Dakota, and Kansas must have been doing something right, while those in Connecticut, Massachusetts, New Jersey, and New York must have been doing something not so right.

   Before you jump too readily to this conclusion, however, back up and look at the data from a different angle. When the College Entrance Examination Board announces the annual state-by-state averages on the SAT, it also lists the percentage of high school seniors within each state who took the SAT. This latter listing is apparently offered only as background information—at any rate, it is passed over quickly in the announcement and receives scant coverage in the news media. Take a close look at it, however, and you will see that the background it provides is very interesting indeed. Here is the relevant information for 1993 for the eight states we have just mentioned. See if you detect a pattern.

State
 		Percentage
taking SAT
 		Average
SAT score
Iowa
North Dakota
South Dakota
Kansas
 		5
6
6
9
 		1103
1101
1060
1042
Connecticut
Massachusetts
New Jersey
New York
 		88
81
76
74
 		904
903
892
887

   Mirabile dictu! The four states near the top of the list had quite small percentages of high school seniors taking the SAT, while the four states near the bottom had quite large numbers of high school seniors taking it. I think you will agree that this observation raises some interesting questions. For example: Could it be that the 5% of Iowa high school seniors who took the SAT in 1993 were the top 5%? What might have been the average SAT score for Connecticut if the test in that state had been taken only by the top 5% of high school seniors, rather than by (presumably) the "top" 88%? You can no doubt imagine any number of variations on this theme.

   Figure 6.1 shows the relationship between these two variables—percentage of high school seniors taking the SAT versus average state score on the SAT—for all 50 of the states. Within the context of correlation and regression, a two-variable coordinate plot of this general type is typically spoken of as a scatterplot or scattergram. Either way, it is simply a variation on the theme of Cartesian coordinate plotting that you have almost certainly already encountered in your prior educational experience. It is a standard method for graphically representing the relationship that exists between two variables, X and Y, in the case where each particular value of Xi is paired with one particular value of Yi.

Figure 6.1. Percentage of High School Seniors Taking the SAT versus Average Combined State SAT Scores: 1993

 

   For the present example, designating the percentage of high school seniors within a state taking the SAT as X, and the state's combined average SAT score as Y, we would have a total of N = 50 paired values of Xi and Yi. Thus for Iowa, Xi = 5% would be paired with Yi = 1103; for Massachusetts, Xi = 81% would be paired with Yi = 903; and so on for all the other 50 states. The entire bivariate list would look like the following, except that the abstract designations for Xi and Yi would of course be replaced by particular numerical values.

State
 		Xi
Percentage
taking SAT
 		Yi
Average
SAT score
1i
2i

::::i

49i
50i
 		X1
X2

::::i

X49
X50
 		Y1
Y2

::::i

Y49
Y50


The next step in bivariate coordinate plotting is to lay out two axes at right angles to each other. By convention, the horizontal axis is assigned to the X variable and the vertical axis to the Y variable, with values of X increasing from left to right and values of Y increasing from bottom to top.    

   A further convention in bivariate coordinate plotting applies only to those cases where a causal relationship is known or hypothesized to exist between the two variables. In examining the relationship between two causally related variables, the independent variable is the one that is capable of influencing the other, and the dependent variable is the one that is capable of being influenced by the other. For example, growing taller will tend to make you grow heavier, whereas growing heavier will have no systematic effect on whether you grow taller. In the relationship between human height and weight, therefore, height is the independent variable and weight the dependent variable. The amount of time you spend studying before an exam can affect your subsequent performance on the exam, whereas your performance on the exam cannot retroactively affect the prior amount of time you spent studying for it. Hence, amount of study is the independent variable and performance on the exam is the dependent variable.

   In the present SAT example, the percentage of high school seniors within a state who take the SAT can conceivably affect the state's average score on the SAT, whereas the state's average score in any given year cannot retroactively influence the percentage of high school seniors who took the test. Thus, the percentage of high school seniors taking the test is the independent variable, X, while the average state score is the dependent variable, Y. In cases of this type, the convention is to reserve the X axis for the independent variable and the Y axis for the dependent variable. For cases where the distinction between "independent" and "dependent" does not apply, it makes no difference which variable is called X and which is called Y.

   In designing a coordinate plot of this type, it is not generally necessary to begin either the X or the Y axis at zero. The X axis can begin at or slightly below the lowest observed value of Xi, and the Y axis can begin at or slightly below the lowest observed value of Yi.

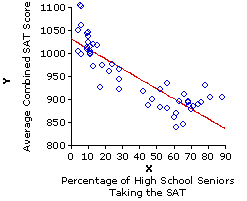
In Figure 6.1b the X axis does begin at zero, because any value much larger than that would lop off the lower end of the distribution of Xi values; whereas the Y axis begins at 800, because the lowest observed value of Yi is 838.

   At any rate, the clear message of Figure 6.1 is that states with relatively low percentages of high school seniors taking the SAT in 1993 tended to have relatively high average SAT scores, while those that had relatively high percentages of high school seniors taking the SAT tended to have relatively low average SAT scores. The relationship is not a perfect one, though it is nonetheless clearly visible to the naked eye. The following version of Figure 6.1 will make it even more visible. It is the same as shown before, except that now we include the straight line that forms the best "fit" of this relationship.We will return to the meaning and derivation of this line a bit later.

   Toggle!
Actually, in this particular example there are two somewhat different patterns that the 50 state data points could be construed as fitting. The first is the pattern delineated by the solid downward slanting straight line, and the second is the one marked out by the dotted and mostly downward sloping curved line that you will see if you click the line labeled "Toggle!" [Click "Toggle!" again to return to the straight line.]
 
A relationship that can be described by a straight line is spoken of as linear (short for 'rectilinear'), while one that can be described by a curved line is spoken of as curvilinear. Our present coverage will be confined to linear correlation.

   Figure 6.2 illustrates the various forms that linear correlation is capable of taking. The basic possibilities are: (i) positive correlation; (ii) negative correlation; and (iii) zero correlation. In the case of zero correlation, the coordinate plot will look something like the rather patternless jumble shown in Figure 6.2a, reflecting the fact that there is no systematic tendency for X and Y to be associated, either the one way or the other. The plot for a positive correlation, on the other hand, will reflect the tendency for high values of Xi to be associated with high values of Yi, and vice versa; hence, the data points will tend to line up along an upward slanting diagonal, as shown in Figure 6.2b. The plot for negative correlation will reflect the opposite tendency for high values of Xi to be associated with low values of Yi, and vice versa; hence, the data points will tend to line up along a downward slanting diagonal, as shown in Figure 6.2d.

Figure 6.2. Various Forms of Linear Correlation


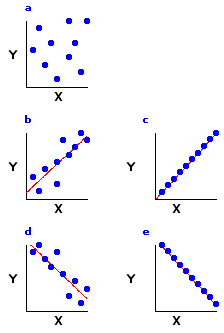The limiting case of linear correlation, as illustrated in Figures 6.2c and 6.2e, is when the data points line up along the diagonal like beads on a taut string. This arrangement, typically spoken of as perfect correlation, would represent the maximum degree of linear correlation, positive or negative, that could possibly exist between two variables. In the real world you will normally find perfect linear correlations only in the realm of basic physical principles; for example, the relationship between voltage and current in an electrical circuit with constant resistance. Among the less tidy phenomena of the behavioral and biological sciences, positive and negative linear correlations are much more likely to be of the "imperfect" types illustrated in Figures 6.2b and 6.2d.

Go to Part 7 [The Measurement of Correlation]