Psychology 105
Richard Lowry
©1999-2002
Some Basic Statistical Concepts and Methods
for the Introductory Psychology Course
Part 9
The Significance of an Observed Correlation
  "How often things occur by the merest chance."
  —Terence, Phormio

   Below this text, in the larger of the two boxes, is a matrix of 4x4=16 squares. When you click the line labeled "Click!", some of these squares will become blue and some will become white. Each time you click the line, any particular one of the 16 squares has a 50% chance of becoming blue and a 50% chance of becoming white. Any pattern that seems to emerge is therefore not the result of design, but derives instead from nothing other than "the merest chance." Yet, if your eye is anything like mine, you will find "organized" patterns emerging on almost every click.




Click!

      Total number of possible
      blue/white combinations:
         216 = 65,536

      Probability of any particular
      blue/white combination:
         0.516 = 0.000,015

   The moral of this demonstration is that the naked eye of common sense cannot readily distinguish between what is the result of mere chance and what is not. The logical and mathematical apparatus of "statistical significance" is a kind of lens through which we can perceive that distinction more clearly and rationally. For the present, our consideration of the topic will be limited to the context of correlation. I'll be introducing you to other aspects of it from time to time in class.

   Here is the moral of our random-patterns demo transplanted to the domain of correlation: it is possible, by the merest chance, to obtain rather impressive-looking values of r within a sample, even when there is no correlation at all within the population from which the sample is taken. This is especially true when the size of the sample is small, but decreasingly so as the size of the sample increases. (The distinction between sample and population is defined in Part 5.)

   The following is a simple experiment by which you can gain some hands-on experience with the principle to which this statement is referring. If you repeatedly toss a pair of dice, there is no reason to expect that the paired outcomes of the dice would be correlated. Another way of saying it is that the correlation within the entire potential population of paired dice outcomes is simply
r[population]=0
Now for the experiment. For each of its two phases you will need a pair of dice, preferably of different colors. One of the dice is designated as X and the other as Y.
Phase I. Toss the dice together 5 times, recording for each toss the number that comes up for X and the number that comes up for Y. The possibilities are of course 1, 2, 3, 4, 5, or 6 for each of the two dice on each toss. Then calculate the correlation coefficient for your 5 XiYi pairs. Record this calculated value of r, and then repeat the whole operation again and again, for as many times as you have the energy and patience If you feel foolish while doing it, keep reminding yourself that you are not merely tossing dice. What you are really doing is collecting a multiplicity of random bivariate samples, each of size N=5, from a population for which you already know the overall correlation to be zero And what you are almost certainly going to find is that, while your numerous sample correlation coefficients will probably average out to about zero, quite a few of them will deviate from this average by a considerable margin.
Phase II. Now do the same thing as in Phase I, but this time make your samples of size N=10. Here again you will find that some of your sample values of r deviate quite markedly from the central value of zero—but now, with this larger sample size, the tendency to deviate is considerably reduced. In order to get a clear idea of the principles that are being illustrated by this two-part experiment, you will need to perform each part at least a hundred times, and preferably many more than a hundred times.
   A few years ago I have had the students in several of my statistics classes perform these exercises, and in the process collected one batch of 473 correlation coefficients, each based on a sample of N=5 paired dice outcomes, and another batch of 424 correlation coefficients, each based on a sample of N=10 paired dice outcomes. The distributions of these two batches of sample correlation coefficients are shown in Figure 9.1. For purposes of illustration, the portions of the two histograms representing sample values of r that deviated from the central value of zero by as much as ±0.50 are marked off and colored in light blue. As you can see, these blue areas of the distributions include nearly 40% of the correlation coefficients based on samples of size N=5 (Figure 9.1a), but only about 12% of those based on samples of size N=10 (Figure 9.1b).

Figure 9.1. Observed Distributions of Random Values of r Drawn from Populations for which r[population]=0

9.1a

9.1b


   The somewhat jagged outlines of the distributions shown in Figure 9.1 are explained by the fact that our batches of 473 and 424 samples, although large in terms of time and effort, are still relatively small in comparison with the number of samples that could have been taken, if only my students had been willing to make a life-time commitment to the experiment. Luckily for both them and me, this life-long labor is not really necessary, since the true forms of these distributions of sample values of r are already known. The knowledge of them comes not from anyone actually observing several hundred million paired dice outcomes, but from logical and mathematical reasoning grounded on the theory of probability.

   Although the process begins with a question that seems highly abstract and hypothetical, the result that comes from it has a very wide range of practical application. Imagine a population of XiYi pairs—paired dice outcomes, or anything else—for which the overall correlation is zero If you were to draw a vast number of bivariate samples from that population, each sample of size N=5, and calculate the correlation coefficient for each sample, and then lay all of these sample values of r out in the form of a relative frequency distribution—what would that distribution look like?

   The answer to this question is depicted in Figure 9.2a, which you will see looks very much like the distribution of 473 sample values of r shown in Figure 9.1a, except that it is smoother and precisely symmetrical. Here again, as a convenient reference point, the portion of the distribution representing sample values of r that would deviate from the central value of zero by as much as ±0.50 are marked off and colored in light blue. As indicated, this would include about 40% of the distribution. That is, about 20% of your multitude of sample correlation coefficients would be as large or larger than +0.50 in the positive direction, and about 20% would be as large or larger than —0.50 in the negative direction. Another way of putting it is that any particular one of the samples has about a 20% likelihood of coming out, by mere chance, with a correlation coefficient equal to or greater than +0.50 in the positive direction, and about a 20% likelihood of coming out, by mere chance, with a correlation coefficient equal to or greater than —0.50 in the negative direction. The principle applies not just to the tossing of dice, but to bivariate situations in general where (i) the correlation within the entire population iszero, and (ii) the samples drawn from the population are of size N=5.

Figure 9.2. Theoretical Distributions of Random Values of r (N=5 and N=10) Drawn from Populations for which r[population]=0

9.2a

9.2b



   Figure  9.2b shows the same type of theoretical distribution for the case where the correlation within the entire population is zero and the samples are of size N=10. Here as well, you can see that the theoretical distribution for samples of size N=10 looks very much like the corresponding distribution of 424 actual samples (Figure 9.1b), except that it is smoother and precisely symmetrical. In this situation only about 12% of the sample values of r would deviate from zero by as much as ±0.50. Half of this 12% would fall at or beyond +0.50 in the positive direction, and the other half would fall at or beyond —0.50 in the negative direction. Alternatively, you can say that any particular one of the samples has about a 6% likelihood of coming out, by mere chance, with a correlation coefficient equal to or greater than +0.50 in the positive direction, and about a 6% likelihood of coming out, by mere chance, with a correlation coefficient equal to or greater than —0.50 in the negative direction.

   You have probably already noticed that the outline of the distribution shown in Figure 9.2b looks like a somewhat squat version of a normal distribution. In fact, it is not a normal distribution; though as you can see from the graphs in Figure 9.3, below, theoretical distributions of this general type do come closer and closer to the form of a normal distribution as you increase the size of the samples. By the time you reach a sample size of N=30 (Figure 9.3b), the shape of the distribution of sample correlation coefficients is virtually identical to that of a normal distribution. Notice also in these two remaining graphs that increasing the size of the samples decreases even further the tendency of sample correlation coefficients to deviate from the zero correlation that exists within the population from which the samples are drawn. Thus, for samples of size N=20 (Figure 9.3a) it is only 2.5% of the sample values of r that will deviate from zero by as much as ±0.50, and for samples of size N=30 (Figure 9.3b) it is only 0.5%.

Figure 9.3. Theoretical Distributions of Random Values of r (N=20 and N=30) Drawn from Populations for which r[population]=0

9.3a

9.3b



   Consider, now, the following hypothetical scenario. Suppose we were to frame the hypothesis that two psychological variables, X and Y, are positively correlated within the general population of current Vassar students. As we do not have the resources for studying each and every member of the current Vassar student population, we resort instead to the strategy of sampling. We select at random a certain number of Vassar students, measuring X and Y for each; and we then calculate a correlation coefficient, which we find to be r=+.50. In short, our hypothesis of a positive correlation within the general population of Vassar students has led us to expect a positive correlation within the sample, and that is exactly what we found.

   Now comes the question of statistical significance, which boiled down to its barest bones is simply this. Given that impressive-looking correlations can occur within limited samples, even when there is no correlation at all between X and Y in the larger reality beyond the sample, what confidence can we have that the +0.50 correlation observed in this particular case is not just a fluke of mere chance coincidence?

   Clearly, the answer to this question depends on the size of the sample—which in our description of this hypothetical scenario was deliberately left unspecified. If the size of the sample is N=5, we would have a 20% chance of observing a positive correlation coefficient as large as +0.50 even if the correlation within the entire population is merely zero. With a sample of size N=10 it drops to a 6% chance; for N=20 it falls further to a scant 1.25% chance; and for N=30 it falls even further to a minuscule one-quarter of one percent. In brief: the larger the size of our sample, the more confidence we can have that our observed correlation of r=+0.50 is not just a fluke of mere chance coincidence.

   As mentioned briefly in Part 1, the cut-off point for statistical significance in most areas of scientific research is conventionally set at the 5% level. That is, an observed result is regarded as statistically significant—as something more than a mere fluke—only if it had a 5% or smaller likelihood of occurring by mere chance coincidence. Otherwise, it is regarded as statistically non-significant. For whatever immediate need you might have to assess the significance of a correlation coefficient, you will be able to get by with the information presented below in Table 9.1 and in Figure 9.4. Table 9.1 shows the positive or negative values of r that are required for statistical significance at the 5% level for various sample sizes, from N=5 through N=32, and for two different kinds of situations to be described below. Figure 9.4 shows the same information in graphic form, but extended across a wider range of sample sizes, from N=5 to N=100.

Table 9.1. Positive or Negative Values of r Required for Statistical Significance at the 5% Level, for Samples of Size N=5 through N=32
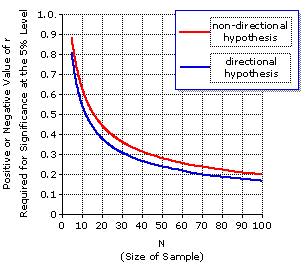
For any particular sample size, an observed value of r is regarded as statistically significant at the 5% level if and only if its distance from zero is equal to or greater than the distance of the tabled value of r. Thus, for a sample of size N=20, an observed value of r=+0.40 or r=—0.40 would be significant at the 5% level for a directional hypothesis, but non-significant for a non-directional hypothesis; an observed value of r=+0.44 or r=—0.44 would be significant for both kinds of hypotheses; and an observed value of r=+0.37 or r=—0.37 would be non-significant for both kinds of hypotheses. (Tabled values of r are rounded to two decimal places.)
Hypothesis
 		Hypothesis
Directional
 		Non-
Directional
 		Directional
 		Non-
Directional
N
 		± r
 		± r
 		N
 		± r
 		± r
5
6
7
8
9
10
11
12
13
14
15
16
17
18
 		0.81
0.73
0.67
0.62
0.58
0.55
0.52
0.50
0.48
0.46
0.44
0.43
0.41
0.40
 		0.88
0.81
0.75
0.71
0.67
0.63
0.60
0.58
0.55
0.53
0.51
0.50
0.48
0.47
 		19
20
21
22
23
24
25
26
27
28
29
30
31
32
 		0.39
0.38
0.37
0.36
0.35
0.34
0.34
0.33
0.32
0.32
0.31
0.31
0.30
0.30
 		0.46
0.44
0.43
0.42
0.41
0.40
0.40
0.39
0.38
0.37
0.37
0.36
0.36
0.35


Figure 9.4. Values of r Required for Statistical Significance at the 5% Level, for Samples of Size N=5 through N=100
    

   The difference between the two kinds of situations is defined by the investigator's hypothesis, which is either directional or non-directional. Within the context of correlation, a directional hypothesis is one that leads the investigator to specify, in advance, one or the other of the following expectations:
POSITIVE DIRECTIONAL HYPOTHESIS: the relationship between X and Y in the general population is positive (the more of X, the more of Y), hence this particular sample of XiYi pairs will show a positive correlation;
or
NEGATIVE DIRECTIONAL HYPOTHESIS: the relationship between X and Y in the general population is negative (the more of X, the less of Y), hence this particular sample of XiYi pairs will show a negative correlation.

A non-directional hypothesis, on the other hand, leads only to the expectation that the correlation between X and Y within the general population might be something other than zero, with no specification of the particular direction in which it might go. Essentially, it is an either-or combination of the two types of directional hypothesis:
NON-DIRECTIONAL HYPOTHESIS: the relationship between X and Y in the general population is something other than zero, hence this particular sample of XiYi pairs will show a non-zero correlation, either positive or negative, though we have no basis for predicting just which of these it will be.

   The important logical difference between these two kinds of situations is that a non-directional hypothesis could potentially be supported by finding either a positive or a negative correlation within the sample, whereas a directional hypothesis could be supported only by finding a correlation within the sample that is in the direction specified; that is, only by finding a positive correlation when the positive direction has been specified, and only by finding a negative correlation when the negative direction has been specified. This logical difference between the two situations entails a different standard of statistical significance. Specifically, for any particular sample size, the value of r required for significance at the 5% level is larger for a non-directional hypothesis than for a directional hypothesis. You need not worry just yet about the detailed rationale of this point. For the moment, it is sufficient to understand the basic distinction between directional and non-directional hypotheses, and to know that the standard of statistical significance for a non-directional hypothesis is more stringent.

   In our imaginary study of the relationship between psychological variables X and Y among Vassar students, we specified in advance that we expected the correlation to be positive. Hence, the applicable standard of statistical significance is the one that pertains to directional hypotheses. If the sample in this study was only of size N=5, the required value of r (see Table 9.1) would be +0.81; so the observed correlation of +0.50, falling short of this required value, would be non-significant. It would also fall short of the required values for a sample of size N=6, 7, 8, 9, 10, or 11. For a sample of size N=12, however, the observed value of +0.50 hits the required value dead center; so for a sample of this size, the observed correlation coefficient would be significant precisely at the 5% level. For any sample size larger than N=12, the observed value of +0.50 would be larger than the required value, and so it would be significant even beyond the 5% level.

   For our earlier SAT example we had a sample of size N=50 and an observed correlation coefficient of r=—0.86. We might conceivably have had some reason to specify a negative directional hypothesis in advance of examining the data—but as we did not, in fact, make that specification, the applicable standard must be the one for a non-directional hypothesis. Here the relevant information is found in Figure 9.4. Start at the horizontal axis where N is equal to 50; go straight up to the red line, which refers to the standard of significance for a non-directional hypothesis; then go straight across to the left to find the required value of r on the vertical axis. That required value is r=±0.28, which means that for a sample of size N=50 and a non-directional hypothesis, an observed correlation coefficient of either r=+0.28 or r=—0.28 would be significant precisely at the 5% level, and that an observed r greater than +0.28 in the positive direction, or greater than —0.28 in the negative direction, would be significant beyond the 5% level. Our actually observed correlation coefficient of r=—0.86 is therefore significant beyond the 5% level.

[End of Quantitative Materials Booklet]