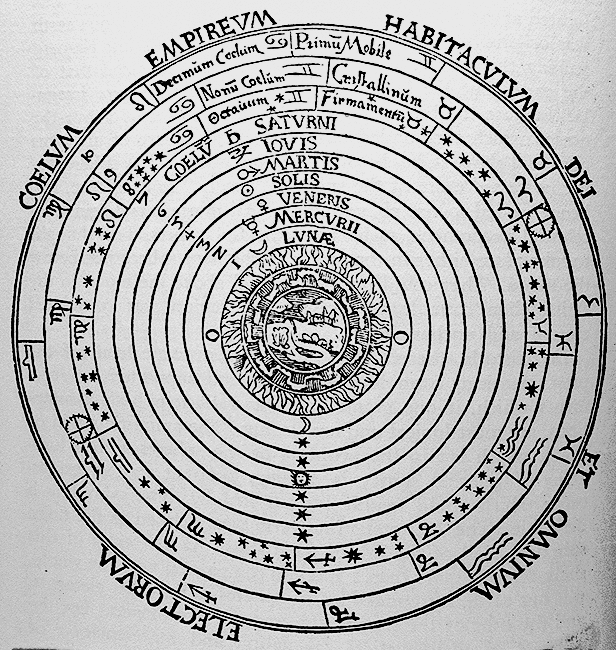
Below is an image of the universe as conceived of by Aristotle and Ptolemy.  The earth is composed of four elements:  Earth, Water, Fire and Air.  It is in the center (notice the trees, mountains and water).  In this cosmology, the earth does not revolve around anything else or rotate around its own axis.  It is surrounded by ten concentric spheres made of a perfectly transparent substance known as "quintessence."  These spheres revolve around the earth, carrying the other celestial bodies.  As you can see, one is the sphere "of the Moon" ("Lunae"), two is Mercury ("Mercurii"), three is Venus ("Veneris"), four is the Sun ("Solis"), five is Mars ("Martis"), six is Jupiter ("Iovis"), seven is Saturn ("Saturni"), and spheres eight, nine and ten hold the "fixed stars" (so-called because they do not move relative to each other, unlike the planets, which move among the other stars).  (The symbols by the names of the planets are the traditional astrological symbols for them.  The symbols in spheres eight, nine and ten are for the twelve astrological constellations, Gemini, Ares, etc.)  Beyond the tenth sphere is, as the words in the periphery say in Latin, "The Kingdom of Heaven, the Abode of God and of the Elect."  (There is more text and and images below.  Keep reading.)

As Thomas Kuhn points out, especially in his book The Copernican Revolution, the Aristotelian Ptolemaic system was remarkably plausible and powerful as a scientific theory.  It intuitively explained our observations:  the Earth does NOT seem to revolve or rotate, while the the moon, the Sun, and the "fixed stars" seem to be revolving around us.

With some minor adjustments, this theory could also account for the puzzling phenomenon of "retrograde motion."  "Planets" means "wanderers."  The planets are called this because they move independently of the fixed stars.  In addition, the planets sometimes seem to reverse their motion.  Ptolemy explained this with "epicycles."  (See the image below, and the explanation beneath the image.)

"E" is the Earth.  "P" is a planet.  The primary orbit of the planet is the circle centered on E.  But there is a secondary circle, an epicycle, whose center (A) is on a point on the primary orbit.  Imagine the primary circle moving counter-clockwise around E, and the secondary circle also moving counter-clockwise around the point A.  From the perspective of the Earth, it will appear that P first moves counter-clockwise (as P moves on its epicycle toward the primary orbit).  Then it will seem to slow down (as P comes closer and closer to the primary orbit).  Finally, P will appear to reverse its motion (as it passes through the primary orbit).  (Technically speaking, whether retrograde motion occurs depends on the relative speed of the orbit and the epicycle, but Ptolemy figured out what the speeds would have to be to account for the motions we do in fact observe.)

This may seem implausibly complicated to you now.  But if you tried to account for the actual motion of the planets according to Newtonian dynamics, you'd find it at least as complicated (just in a different way).